Search 2D Matrix in a better way

 

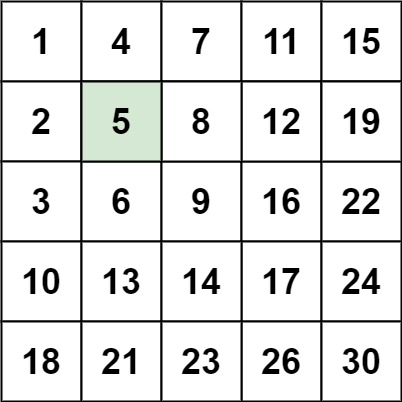
Below implement a C++ program that user fewer steps than binary search algorithm for search in 2-dimensional integer matrix(array).It can be used to search array like above figure.

CODE

#include <iostream>

using namespace std;
//I define 5*5 matrix..But by this algorithm you can perform other sizes also.But need to declare in the algorithm
int const rows = 5;   //define matrix No.of Rows...
int const columns = 5; //define matrix No.of Columns...

//function of seaching elements....
void binarySearch(int matrix[5][5], int x, int start, int last, int counting, int k3, int steps[5][5], int k1, int k2, int rows)
{
    while (start <= last) //check to stop searching...
    {
        int mid = last - (last - start) / 2;  //find middle element
        counting = counting + 1;   //counting steps...

        if (matrix[k3][mid] == x)
        {

            steps[k1][k2] = counting;  //asign the counting to steps array...
            k3 = rows;   //if element found then to stop main funtion loop...

        }
        else if (x < matrix[k3][mid])  //if searching element less than checking element..
        {
            last = mid - 1;
            binarySearch(matrix, x, start, last, counting, k3, steps, k1, k2, rows);  //recursively call
        }
        else            //if searching element greater than checking element..
        {       
            start = mid + 1;  
            binarySearch(matrix, x, start, last, counting, k3, steps, k1, k2, rows);  //recursively call
        }


    }

}


int main()
{
    int matrix[rows][columns];
    cout << "Enter Matrix Elements row by row(**Please make sure each elements that entered are Unique) : " << endl;
    for (int i = 0; i < rows; i++)
    {
        cout << "Enter Row " << i + 1 << " Elements : " << endl;
        for (int j = 0; j < columns; j++)  //matrix input...
        {
            cin >> matrix[i][j];
        }
    }


    //SORT ROWS....
    for (int r = 0; r < rows; r++)
    {
        for (int i2 = 1; i2 < columns; i2++) {
            for (int j2 = 0; j2 < i2; j2++) {
                int c2 = matrix[r][i2];
                if (matrix[r][i2] < matrix[r][j2]) {
                    matrix[r][i2] = matrix[r][j2];
                    matrix[r][j2] = c2;
                }
            }
        }
    }


    //SORT COLUMNS.....
    for (int c = 0; c < columns; c++)
    {
        for (int i1 = 1; i1 < rows; i1++) {
            for (int j1 = 0; j1 < i1; j1++) {
                int c1 = matrix[i1][c];
                if (matrix[i1][c] < matrix[j1][c]) {
                    matrix[i1][c] = matrix[j1][c];
                    matrix[j1][c] = c1;
                }
            }
        }
    }


    int start = 0;
    int last = columns - 1;
    int steps[5][5];  //steps array....
   
    for (int k1 = 0; k1 < rows; k1++)   //count each element steps...
    {
        for (int k2 = 0; k2 < columns; k2++)
        {
            int count = 0;

            for (int k3 = 0; k3 < rows; k3++)
            {
                binarySearch(matrix, matrix[k1][k2], 0, columns - 1, count, k3, steps, k1, k2, rows);  //call the binary search function...
            }

        }


    }
    
    int increment[rows]; //array of highest number each row ...
    //this is to find the highest steps in each row...
    for (int r1 = 0; r1 < rows; r1++)
    {
        int c = steps[r1][0];
        for (int r2 = 1; r2 < columns; r2++)
        {
            if (c <= steps[r1][r2])
            {
                c = steps[r1][r2];
            }
        }
        increment[r1] = c;

    }
    //this is for adding above row steps for below row(described in the text file)
    for (int m = 1; m < rows; m++)
    {
        increment[m] = increment[m] + increment[m - 1];
    }

    //modify counted steps...
    for (int n1 = 1; n1 < rows; n1++)
    {
        for (int n2 = 0; n2 < columns; n2++)
        {
            steps[n1][n2] = steps[n1][n2] + increment[n1 - 1];
        }
    }
    //output each elements, steps....
    int t = 0;
    cout << endl << endl;
    cout << "Steps for Each Element : " << endl;
    for (int w1 = 0; w1 < rows; w1++)
    {
        for (int w2 = 0; w2 < columns; w2++)
        {
            t = t + steps[w1][w2];
            cout << "Searching Item : " << matrix[w1][w2] << "   Number of Steps : " << steps[w1][w2] << endl;
        }
        
    }
    //average steps for searching in the 2D matrix....
    cout << endl << "Average Steps : " << t / 25.0;


    return 0;
}

 

 

Explanation

• First I perform binary search on each row and count each element searching steps in that row
• By that I got steps for each element(but steps that I got are if there is only one row)
• So I counted each row highest seaching step(because if below element seach in a above row it won't found but, it want to seaching each row by row..)
• So I adding that previous row highest searching step to below row each element seaching steps(and accordingly in last row each element consisting above all rows highest steps for each element)
• Finally output total each elements searching steps
• I got 8.92 average step using binary search and by this algorithm I got 8.2 average step